抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

VNCTF Crypto wp

crypto比赛

发布于：2025年2月9日

次浏览

Simple prediction

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
from random import shuffle
from Crypto.Util.number import getPrime
from random import choice, randint
from secret import *

# flag来源
flag = b"VNCTF{xxxxxxx}"
assert len(flag)<100
FLAG1=flag[:32]
FLAG2=flag[32:]

# part1
class LCG:
    def __init__(self, seed=None, a=None, b=None, m=None):
        if not m:
            self.m = getPrime(512)
        if not seed:
            self.seed = getPrime(512)
        if not a:
            self.a = getPrime(512)
        if not b:
            self.b = getPrime(512)
        #print(f"LCG 初始化参数: seed={self.seed}\n a={self.a}\n b={self.b}\n m={self.m}")

    def next(self):
        self.seed = (self.seed * self.a + self.b) % self.m
        return self.seed
binary_flag = ''.join(f"{byte:08b}" for byte in FLAG1)
m = [int(bit) for bit in binary_flag]

n=[]
lcg=LCG()

for i in m:
    z=lcg.next()
    if i == 0:
        n.append(z)
    else:
        z=randint(0, 2**512)
        n.append(z)
print(f"n={n}")

'''
n有点长，这边我就不放了
'''

# part2
class FlagEncoder:
    def __init__(self, flag: bytes, e: int = 65537):
        self.flag = flag
        self.e = e
        self.encoded_flag = []
        self.n = None
        self.c = None

    def process(self):
        for idx, byte in enumerate(self.flag):
            self.encoded_flag.extend([idx + 0x1234] * byte)
        shuffle(self.encoded_flag)
        p, q = getPrime(1024), getPrime(1024)
        self.n = p * q
        self.c = sum(pow(m, self.e, self.n) for m in self.encoded_flag) % self.n
        print(f"{self.n = }\n{self.e = }\n{self.c = }\n")

encoder = FlagEncoder(FLAG2)
encoder.process()

'''
self.n = 16880924655573626811763865075201881594085658222047473444427295924181371341406971359787070757333746323665180258925280624345937931067302673406166527557074157053768756954809954623549764696024889104571712837947570927160960150469942624060518463231436452655059364616329589584232929658472512262657486196000339385053006838678892053410082983193195313760143294107276239320478952773774926076976118332506709002823833966693933772855520415233420873109157410013754228009873467565264170667190055496092630482018483458436328026371767734605083997033690559928072813698606007542923203397847175503893541662307450142747604801158547519780249
self.e = 65537
self.c = 9032357989989555941675564821401950498589029986516332099523507342092837051434738218296315677579902547951839735936211470189183670081413398549328213424711630953101945318953216233002076158699383482500577204410862449005374635380205765227970071715701130376936200309849157913293371540209836180873164955112090522763296400826270168187684580268049900241471974781359543289845547305509778118625872361241263888981982239852260791787315392967289385225742091913059414916109642527756161790351439311378131805693115561811434117214628348326091634314754373956682740966173046220578724814192276046560931649844628370528719818294616692090359
'''

题目基于两部分加密，第一部分是一个决策形LCG，没什么难的，只要还原出a b m seed就可以进行判断

这四个我们可以通过gro来还原

exp1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from Crypto.Util.number import long_to_bytes, isPrime, inverse

FLAG1 = b"VNCTF{"
binary_flag = ''.join(f"{byte:08b}" for byte in FLAG1)
sample = [int(bit) for bit in binary_flag]
n = [] #####
PR = PolynomialRing(ZZ, names = ['seed', 'a', 'b'])
seed, a, b = PR.gens()
poly = []
tmp = seed
for idx, val in enumerate(sample):
    tmp = a * tmp + b 
    if val == 0:
        poly.append(tmp - n[idx])
Ideal(poly).groebner_basis()
'''
[seed + 2165903508073506623994838827066532958941139554558794270016694649783805145530913119818321131856946871239910300387306903547575263070144295368326573844536005, a + 429873896302458910672986962586276737599414094876069899060035489494025286474462816078224557288966599271476609468200373372521963415875150647376511007465212, b + 1589404022992814210771169508378145412844556443333866647707390024788331812145300690677773046411734443033110788720862387777824656124349529846537194036826450, 10916943396243271758266829435555189967315413084893315714705045128417174415341289341427433287377943483933876693839607971139318822507789476490876054697833171]
'''
m = 10916943396243271758266829435555189967315413084893315714705045128417174415341289341427433287377943483933876693839607971139318822507789476490876054697833171
a = -429873896302458910672986962586276737599414094876069899060035489494025286474462816078224557288966599271476609468200373372521963415875150647376511007465212 % m
b = -1589404022992814210771169508378145412844556443333866647707390024788331812145300690677773046411734443033110788720862387777824656124349529846537194036826450 % m
seed = (n[0] - b) * inverse(a, m) % m


assert isPrime(m)
assert isPrime(a)
assert isPrime(b)
# assert isPrime(seed)



tmp = seed
flag1 ='' 
for i in n:
    tmp = (a * tmp + b) % m
    if tmp == i:
        flag1 += '0'
    else:
        flag1 += '1'
print(long_to_bytes(int(flag1, 2))) #

第二部分本质上是一个背包

具体做法可以见下面这题，一样的，我记得是当时在crewctf里面做过

还有这题，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from random import shuffle
from Crypto.Util.number import getPrime


with open('flag.txt', 'rb') as f:
    FLAG = f.read().strip()

assert len(FLAG) < 100

encoded_flag = []

for i, b in enumerate(FLAG):
    encoded_flag.extend([i + 0x1337] * b)

shuffle(encoded_flag)

e = 65537
p, q = getPrime(1024), getPrime(1024)
n = p * q
c = sum(pow(m, e, n) for m in encoded_flag) % n

with open('output.txt', 'w') as f:
    f.write(f'{n = }\n{e = }\n{c = }\n')
image-20240812123822640

但是会发现这个格出不了，那就把n放进去再搞一个格，稍微扩大一下

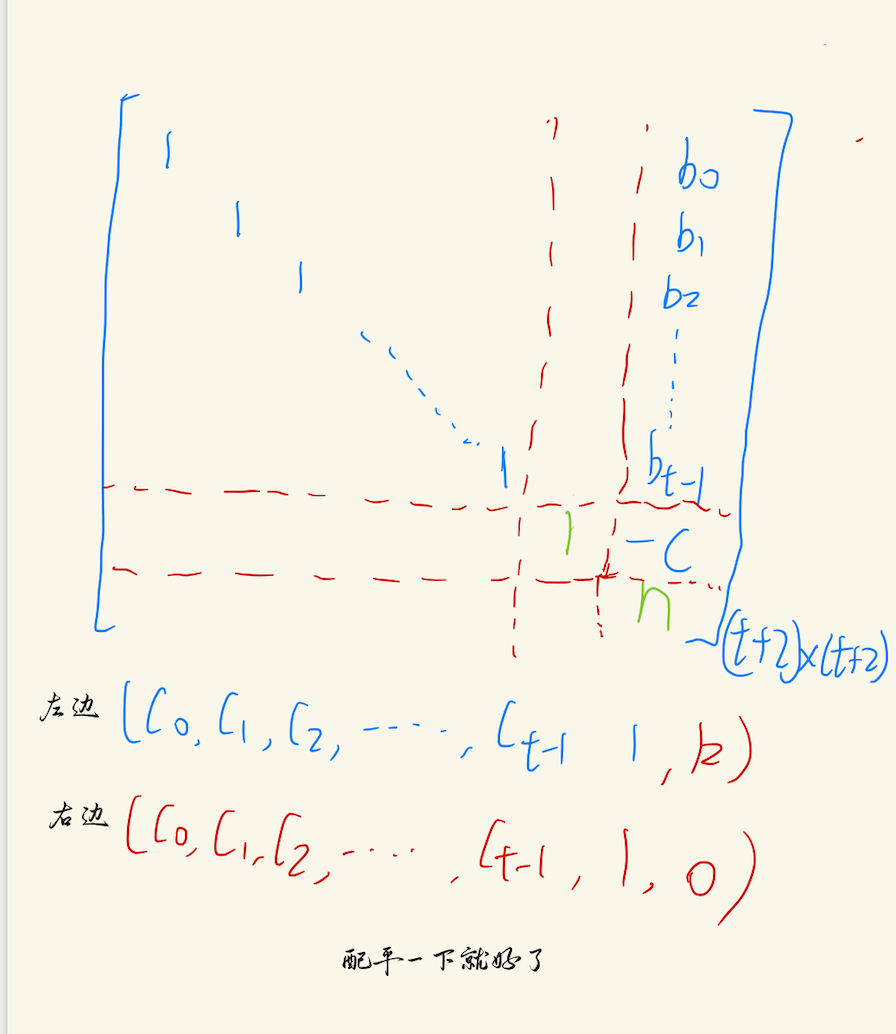
image-20240812123941908

这个格就出了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import long_to_bytes
from tqdm import tqdm
import sys

n = 11570808501273498927205104472079357777144397783547577003261915477370622451850206651910891120280656785986131452685491947610185604965099812695724757402859475642728712507339243719470339385360489167163917896790337311025010411472770004154699635694228288241644459059047022175803135613130088955955784304814651652968093606122165353931816218399854348992145474578604378450397120697338449008564443654507099674564425806985914764451503302534957447420607432031160777343573246284259196721263134079273058943290282037058625166146116257062155250082518648908934265839606175181213963034023613042840174068936799861096078962793675747202733
e = 65537
c = 7173375037180308812692773050925111800516611450262181376565814072240874778848184114081029784942289615261118103256642605595499455054072839201835361613983341298973366881719999836078559255521052298848572778824157749016705221745378832156499718149327219324078487796923208917482260462508048311400560933782289383624341257636666638574026084246212442527379161504510054689077339758167386002420794571246577662116285770044542212097174474572856621921237686119958817024794843805169504594110217925148205714768001753113572920225449523882995273988088672624172009740852821725803438069557080740459068347366098974487213070886509931010623
for t in tqdm(range(100)):
    b = []
    for i in range(t):
        b.append(pow(0x1337 + i, e, n))
    L = block_matrix([[identity_matrix(t), Matrix(ZZ, t, 1), Matrix(ZZ, t, 1, b)], 
                      [Matrix(ZZ, 1, t), 1, -c], 
                      [Matrix(ZZ, 1, t), 0, n]]) * diagonal_matrix(ZZ, [1] * (t + 1) + [n])
    res = L.LLL()
    for i in res:
        if i[-1] == 0:
            new = i[:-2:]
            if all(0 < abs(j) < 255 for j in new):
                flag = ''.join([chr(abs(k)) for k in new])
                if 'crew{' in flag:
                    print(flag)
                    sys.exit()

这边贴个exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from Crypto.Util.number import long_to_bytes
from tqdm import tqdm
import sys

n = 16880924655573626811763865075201881594085658222047473444427295924181371341406971359787070757333746323665180258925280624345937931067302673406166527557074157053768756954809954623549764696024889104571712837947570927160960150469942624060518463231436452655059364616329589584232929658472512262657486196000339385053006838678892053410082983193195313760143294107276239320478952773774926076976118332506709002823833966693933772855520415233420873109157410013754228009873467565264170667190055496092630482018483458436328026371767734605083997033690559928072813698606007542923203397847175503893541662307450142747604801158547519780249
e = 65537
c = 9032357989989555941675564821401950498589029986516332099523507342092837051434738218296315677579902547951839735936211470189183670081413398549328213424711630953101945318953216233002076158699383482500577204410862449005374635380205765227970071715701130376936200309849157913293371540209836180873164955112090522763296400826270168187684580268049900241471974781359543289845547305509778118625872361241263888981982239852260791787315392967289385225742091913059414916109642527756161790351439311378131805693115561811434117214628348326091634314754373956682740966173046220578724814192276046560931649844628370528719818294616692090359
for t in tqdm(range(32, 100)):
    b = []
    for i in range(t):
        b.append(pow(0x1234 + i, e, n))
    L = block_matrix([[identity_matrix(t), Matrix(ZZ, t, 1), Matrix(ZZ, t, 1, b)], 
                      [Matrix(ZZ, 1, t), 1, -c], 
                      [Matrix(ZZ, 1, t), 0, n]]) * diagonal_matrix(ZZ, [1] * (t + 1) + [n])
    res = L.LLL()
    for i in res:
        if i[-1] == 0:
            new = i[:-2:]
            if all(0 < abs(j) < 255 for j in new):
                flag = ''.join([chr(abs(k)) for k in new])
                if flag.isascii():
                    print(flag)
                    sys.exit()

ss0Hurt!

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from Crypto.Util.number import *
from flag import flag

class DaMie:
    def __init__(self, flag , n = None):
        self.m = ZZ(bytes_to_long(flag))
        self.n = n if n else getPrime(1024)
        self.P = Zmod(self.n)
        print(f'n = {self.n}')

    def process(self, x, y, z):

        return vector([5 * x + y - 5 * z, 5 * y - z, 5 * z])

    def Mat(self, m):
        PR = self.P['x,y,z']
        x,y,z = PR.gens()

        if m != 0:
            plana = self.Mat(m//2)
            planb = plana(*plana)
            if m % 2 == 0:
                return planb
            else:
                return self.process(*planb)
        else:
            return self.process(*PR.gens())

    def hash(self, A, B, C):
        return self.Mat(self.m)(A, B, C)

if __name__ == '__main__':
    
    Ouch = DaMie(flag)
    result = Ouch.hash(2025,208,209)
    print(f'hash(A,B,C) = {result}')

xyctf的原题，改了个数据而已，有兴趣可以去搜一下当时的fakeRSA，我这边就贴一下当时那题的做法，照猫画虎即可

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *

flag = b'XYCTF{******}'
n = ZZ(bytes_to_long(flag))
p = getPrime(int(320))
print(p)

G = Zmod(p)

def function(X, Y, Z):
    def part(a, b, c):
        return vector([9 * a - 36 * c, 6 * a - 27 * c, b])
    def parts(n):
        Gx.<a, b, c> = G[]
        if n == 0: 
            return vector([a, b, c])
        mid = parts(n // 2)
        result = mid(*mid)
        if n % 2 == 0: 
            return result
        else: 
            return part(*result)
    return parts(n)(X, Y, Z)

print(function(69, 48, 52))
image-20240406141044360 
1
https://www.wolframalpha.com/input/?i=%7B%7B3%2C1%2C0%7D%2C%7B0%2C3%2C1%7D%2C%7B0%2C0%2C3%7D%7D%5En

计算通项公式

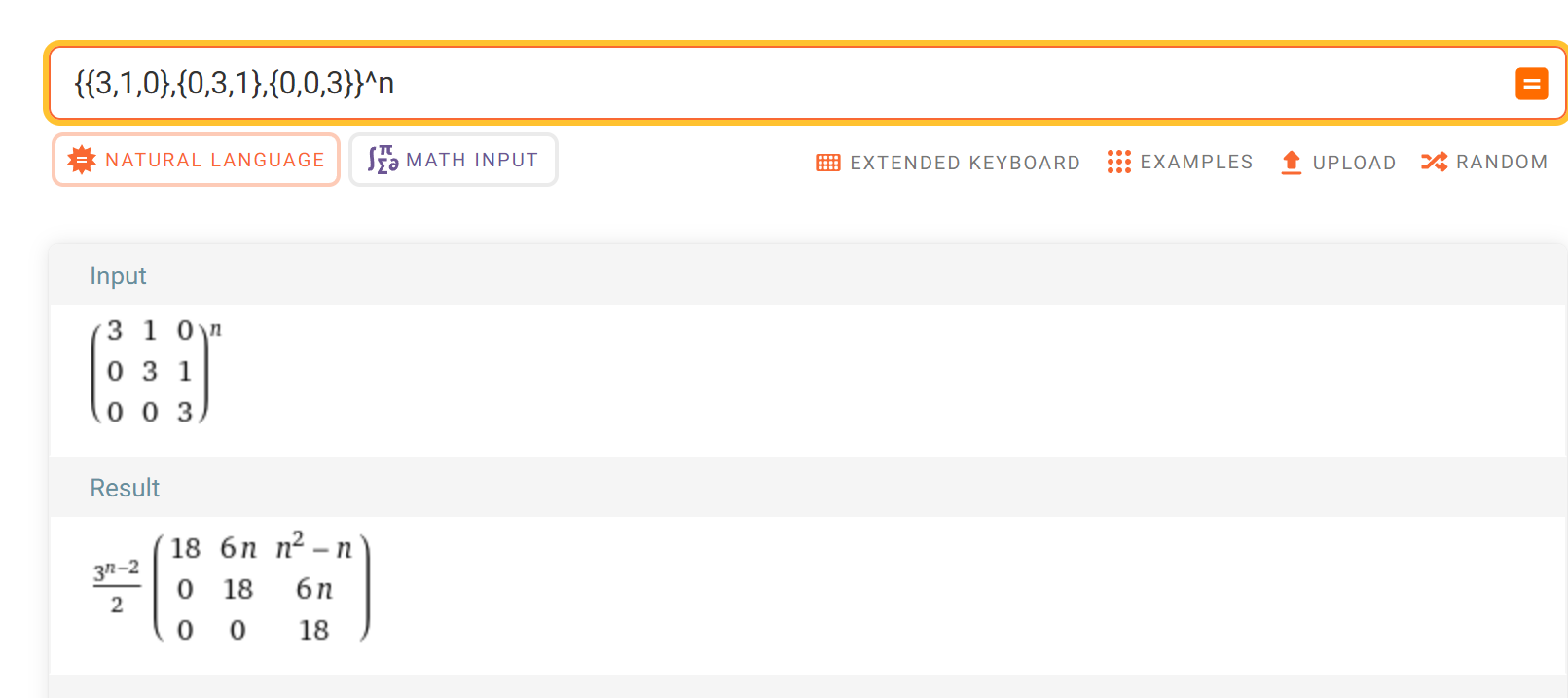
image-20240406141150338

image-20240406141240469 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#sage
from gmpy2 import invert
a = 69
b = 48
c = 52
p = 1849790472911267366045392456893126092698743308291512220657006129900961168811898822553602045875909
A = Matrix(GF(p), [[9, 6, 0],
                   [0, 0, 1], 
                   [-36, -27, 0]])

H = Matrix(GF(p), [a, b, c])

L = Matrix(GF(p), [1431995965813617415860695748430644570118959991271395110995534704629241309597572003500157255135707, 1011565891130611736600822618382801465506651972373410962205810570075870804325974377971089090196019, 784497518859893244278116222363814433595961164446277297084989532659832474887622082585456138030246])


A_Jor, T = A.jordan_form(transformation=True)


D1 = H * T
D2 = L * T


a1, b1, c1 = D1[0, 0], D1[0, 1], D1[0, 2]
a2, b2, c2 = D2[0, 0], D2[0, 1], D2[0, 2]

x = (3 * a1 * b2 - 3 * a2 * b1) * invert(int(a1 * a2), p) % p

print(x)#11248090436223445352625693407089269386223255468324240386169564292825656540049141991068475773
#b'XYCTF{y0u_finally_f0und_t3h_s3cr3ts!!}'


如果这边没有使用数学工具，可以按下面这样进行推导

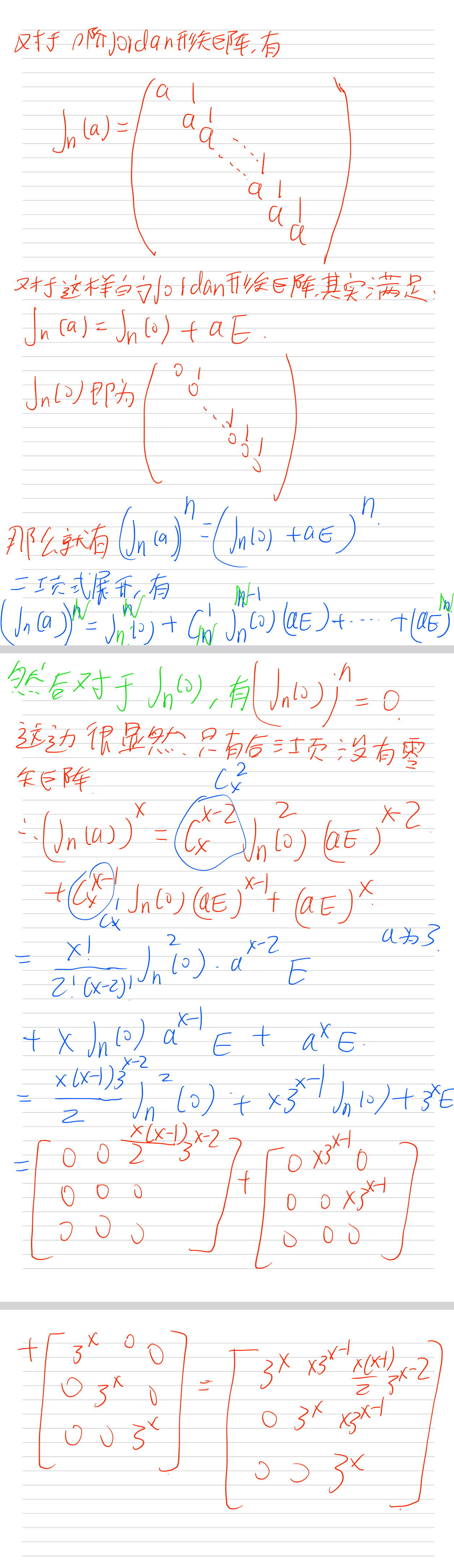
image-20240506172413511

本题exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *
from gmpy2 import invert

x, y, z = 2025,208,209
p = 106743081253087007974132382690669187409167641660258665859915640694456867788135702053312073228376307091325146727550371538313884850638568106223326195447798997814912891375244381751926653858549419946547894675646011818800255999071070352934719005006228971056393128007601573916373180007524930454138943896336817929823
A = Matrix(GF(p), [[5, 0, 0],
                   [1, 5, 0], 
                   [-5, -1, 5]])

H = Matrix(GF(p), [x, y, z])

L = Matrix(GF(p), [17199707718762989481733793569240992776243099972784327196212023936622130204798694753865087501654381623876011128783229020278210160383185417670794284015692458326761011808048967854332413536183785458993128524881447529380387804712214305034841856237045463243243451585619997751904403447841431924053651568039257094910, 62503976674384744837417986781499538335164333679603320998241675970253762411134672614307594505442798271581593168080110727738181755339828909879977419645331630791420448736959554172731899301884779691119177400457640826361914359964889995618273843955820050051136401731342998940859792560938931787155426766034754760036, 93840121740656543170616546027906623588891573113673113077637257131079221429328035796416874995388795184080636312185908173422461254266536066991205933270191964776577196573147847000446118311985331680378772920169894541350064423243733498672684875039906829095473677927238488927923581806647297338935716890606987700071])


A_Jor, T = A.jordan_form(transformation=True)
A_Jor

D1 = H * T
D2 = L * T


a1, b1, c1 = D1[0, 0], D1[0, 1], D1[0, 2]
a2, b2, c2 = D2[0, 0], D2[0, 1], D2[0, 2]

x = (5 * a1 * b2 - 5 * a2 * b1) * invert(int(a1 * a2), p) % p

print(long_to_bytes(int(x)))

b'\xd6NCTF{WWhy_diagonalization_1s_s0_brRRRrRrrRrrrRrRRrRRrrrRrRrRuUuUUUTTTtte3333?????ouch!ouch!Th3t_is_S0_Crazy!!!!}'

easymath

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
from secret import flag
flag=bytes_to_long(flag)
l=flag.bit_length()//3 + 1
n=[]
N=1
while len(n) < 3:
    p = 4*getPrime(l)-1
    if isPrime(p):
        n.append(p)
        N *= p

print(f'c={flag*flag%N}')

from sympy import symbols, expand
x = symbols('x')
polynomial = expand((x - n[0]) * (x - n[1]) * (x - n[2]))

print(f'{polynomial=}')
# c=24884251313604275189259571459005374365204772270250725590014651519125317134307160341658199551661333326703566996431067426138627332156507267671028553934664652787411834581708944
# polynomial=x**3 - 15264966144147258587171776703005926730518438603688487721465*x**2 + 76513250180666948190254989703768338299723386154619468700730085586057638716434556720233473454400881002065319569292923*x - 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619

思路很直接，先使用factor分解得到三个小n，然后在各自的模意义之下进行crt的组合即可

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
x = var('x')
f = x**3 - 15264966144147258587171776703005926730518438603688487721465*x**2 + 76513250180666948190254989703768338299723386154619468700730085586057638716434556720233473454400881002065319569292923*x - 125440939526343949494022113552414275560444252378483072729156599143746741258532431664938677330319449789665352104352620658550544887807433866999963624320909981994018431526620619
f.factor()
#(x - 3868765709106144154703556118635822400623994075212553582411)*(x - 5487564316951417093934647798659941512646442958127439071827)*(x - 5908636118089697338533572785710162817248001570348495067227)


from Crypto.Util.number import *
from gmpy2 import iroot
import sys

n0, n1, n2 = 3868765709106144154703556118635822400623994075212553582411, 5487564316951417093934647798659941512646442958127439071827, 5908636118089697338533572785710162817248001570348495067227
N = n0 * n1 * n2
c = 24884251313604275189259571459005374365204772270250725590014651519125317134307160341658199551661333326703566996431067426138627332156507267671028553934664652787411834581708944
R.<m> = Zmod(n0)[]
f = m ^ 2 - c
res1 = f.roots()

R.<m> = Zmod(n1)[]
f = m ^ 2 - c
res2 = f.roots()

R.<m> = Zmod(n2)[]
f = m ^ 2 - c
res3 = f.roots()


for i in res1:
    for j in res2:
        for k in res3:
            r_n0, r_n1, r_n2 = ZZ(i[0]), ZZ(j[0]), ZZ(k[0])
            flag = int(crt([r_n0, r_n1, r_n2], [n0, n1, n2]))
            if long_to_bytes(int(flag)).isascii():
                print(long_to_bytes(int(flag)))
                sys.exit()

sh1kaku_fw

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from Crypto.Util.number import getPrime 
from sympy import nextprime
from secret import FLAG
import numpy as np
import random
import signal
import os


def _handle_timeout(signum, frame):
    raise TimeoutError('function timeout')

timeout = 450
signal.signal(signal.SIGALRM, _handle_timeout)
signal.alarm(timeout)

def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

n = 197
m = 19700
q = getPrime(20)

e_L = [random.randrange(0, q-1) for i in range(2)]
R_s = random.SystemRandom()
R_e = random.SystemRandom()

s = np.array(uniform_sample(n, q//2, R_s))
e = np.array(choice_sample(m,  e_L, R_e))

seed = os.urandom(16)
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)])
b = (A.dot(s) + e) % q

print(f"{q = }")
print(f"{e_L = }")
print(f"{seed.hex() = }")
print(f"{b.tolist() = }") 

s_ = input("Give me s: ")
if s_ == str(s.tolist()):
    print("Congratulations! You have signed in successfully.")
    print(FLAG)
else:
    print("Sorry, you cannot sign in.")

这题其实和西湖论剑那题很像，只不过这题的数据量实在太大了，很吃配置，一般的笔记本跑不动，sage容易挂掉

所以我简单改了个题目，毕竟复现主要是学习知识

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import getPrime 
from sympy import nextprime
import numpy as np
import random
import os



def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

n = 197
m = 19700
q = getPrime(20)

e_L = [random.randrange(0, q-1) for i in range(2)]
R_s = random.SystemRandom()
R_e = random.SystemRandom()

s = np.array(uniform_sample(n, q//2, R_s))
e = np.array(choice_sample(m,  e_L, R_e))

seed = os.urandom(16)
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)])
b = (A.dot(s) + e) % q

with open('output.txt', 'w') as f:
    
    f.write(f"{q = }\n")
    f.write(f"{e_L = }\n")
    f.write(f"{seed.hex() = }\n")
    f.write(f"{b.tolist() = }\n") 
    f.write(f"{s.tolist() = }")    #这边写入s是用来方便后续的检验的

题目要求就是求出s

先说思路吧，这边会说的比较简单，如果要看详细思路的话可以看我西湖论剑的那题的复现

1
https://suhanhan-cpu.github.io/2025/02/12/2025-%E8%A5%BF%E6%B9%96%E8%AE%BA%E5%89%91-New-Year-Ring4-wp%E5%A4%8D%E7%8E%B0/

这题看起来像lwe的板子，但是实际观察我们会发现，e相对于模数来说并不是小量，而且这题如果要造格的话本身的维度非常的大，这显然是不现实的

首先我们有如下的等式

(a00a01⋯a0196a10a11⋯a1196⋮⋮⋱⋮a196990a196991⋯a19699196)(s0,s1,⋮,s196) + (e0,e1,⋮,e196)=(b0,b1,⋮,b196)\begin{array}{l} \begin{pmatrix} a_{0_0} & a_{0_1} & \cdots & a_{0_{196}} \\ a_{1_0} & a_{1_1} & \cdots & a_{1_{196}} \\ \vdots & \vdots & \ddots & \vdots \\ a_{19699_0} & a_{19699_1} & \cdots & a_{19699_{196}} \end{pmatrix} \begin{pmatrix} s_0,\\ s_1, \\ \vdots,\\ s_{196} \end{pmatrix} \ + \ \begin{pmatrix} e_0,\\ e_1, \\ \vdots,\\ e_{196} \end{pmatrix} = \begin{pmatrix} b_0,\\ b_1, \\ \vdots,\\ b_{196} \end{pmatrix} \end{array}

然后这边的误差向量e都是从e_L这里面随机选择的，根据矩阵乘法的性质，就拿第一组等式来说，我们有

(a00,a01,⋯ ,a0196)(s0,s1,⋮,s196) + e0=b0\begin{array}{l} (a_{0_0} , a_{0_1} , \cdots , a_{0_{196}})\begin{pmatrix} s_0,\\ s_1, \\ \vdots,\\ s_{196} \end{pmatrix} \ +\ e_0 = b_0 \end{array}

那么也就是

∑i=0196si∗ai0−b0+e0=0\sum_{i=0}^{196} s_i * a_{i_0} - b_0 + e_0 = 0

这边我e0e_0是e_L中哪个我们是不知道的，但是无论如何，我们都会有如下的等式

(∑i=0196si∗ai0−b0+e_L[0])∗(∑i=0196si∗ai0−b0+e_L[1])=0(\sum_{i=0}^{196} s_i * a_{i_0} - b_0 + e\_L[0]) * (\sum_{i=0}^{196} s_i * a_{i_0} - b_0 + e\_L[1]) = 0

这样我们就可以从第一组当中拿到一组等式，这边一共有19700组，也就是有19700组等式，现在我们只要看未知项是多少就可以决定能不能求解这个方程组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import long_to_bytes
from ast import literal_eval
from tqdm import tqdm
import numpy as np
import random
import time

start_time = time.time()

def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

with open('output.txt', 'r') as f:
    q = int(f.readline().strip().split(' = ')[1])
    e_L = literal_eval(f.readline().strip().split(' = ')[1])
    seed = long_to_bytes(int(f.readline().strip().split(' = ')[1].strip("\'"), 16))
    b = literal_eval(f.readline().strip().split(' = ')[1])
    answer = literal_eval(f.readline().strip().split(' = ')[1])

n = 197
m = 19700
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)]).tolist()

variables = [f's{i}' for i in range(197)] + ['e']
MY = PolynomialRing(GF(q), variables)
s = vector(MY.gens()[:-1:])
e = MY.gens()[-1]


L, R = [], []
for i in tqdm(range(19700)):
    tmp = (vector(A[i]) * s  + e_L[0] - b[i]) * (vector(A[i]) * s  + e_L[1] - b[i])
    print(len(tmp.monomials()))  #19701，去掉最后的常数项刚好和题目给我们的一样多，这还是很有希望获得方程组的唯一解的
    print(tmp.monomials())
    break


这边是对应的项（这边我们只给出我们所需要使用的那几项，也就是最后的那几项）

1
s0, s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11, s12, s13, s14, s15, s16, s17, s18, s19, s20, s21, s22, s23, s24, s25, s26, s27, s28, s29, s30, s31, s32, s33, s34, s35, s36, s37, s38, s39, s40, s41, s42, s43, s44, s45, s46, s47, s48, s49, s50, s51, s52, s53, s54, s55, s56, s57, s58, s59, s60, s61, s62, s63, s64, s65, s66, s67, s68, s69, s70, s71, s72, s73, s74, s75, s76, s77, s78, s79, s80, s81, s82, s83, s84, s85, s86, s87, s88, s89, s90, s91, s92, s93, s94, s95, s96, s97, s98, s99, s100, s101, s102, s103, s104, s105, s106, s107, s108, s109, s110, s111, s112, s113, s114, s115, s116, s117, s118, s119, s120, s121, s122, s123, s124, s125, s126, s127, s128, s129, s130, s131, s132, s133, s134, s135, s136, s137, s138, s139, s140, s141, s142, s143, s144, s145, s146, s147, s148, s149, s150, s151, s152, s153, s154, s155, s156, s157, s158, s159, s160, s161, s162, s163, s164, s165, s166, s167, s168, s169, s170, s171, s172, s173, s174, s175, s176, s177, s178, s179, s180, s181, s182, s183, s184, s185, s186, s187, s188, s189, s190, s191, s192, s193, s194, s195, s196, 1]

这时候根据等式我们可以构造出如下的矩阵

L(s02s0∗s1⋮s0s1⋮s196)=R\begin{array}{l} L \begin{pmatrix} s_0 ^ 2 \\ s_0 * s_1 \\ \vdots \\ s_0 \\ s_1 \\ \vdots \\ s_{196} \\ \end{pmatrix}= R \end{array}

这边的L中包含着每组等式对应项对应的系数，R是每个多项式对应的常数项移到等式右边也可以构成一个列向量

这样解这个矩阵方程得到sol，再取他最后的196个元素即可拿到私钥s，另外这边因为s是限制在(−q2,q2)(-\frac{q}{2}, \frac{q}{2})之间，所以我们还要遍历当中的每一个元素（因为原先运算都是在模q意义下的），当他大于q2\frac{q}{2}的时候减掉qq就可以了

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from Crypto.Util.number import long_to_bytes
from ast import literal_eval
from tqdm import tqdm
import numpy as np
import random
import time

start_time = time.time()

def uniform_sample(n, bound, SecureRandom):
    return [SecureRandom.randrange(-bound, bound) for _ in range(n)]

def choice_sample(n, L, SecureRandom):
    return [SecureRandom.choice(L) for i in range(n)]

with open('output.txt', 'r') as f:
    q = int(f.readline().strip().split(' = ')[1])
    e_L = literal_eval(f.readline().strip().split(' = ')[1])
    seed = long_to_bytes(int(f.readline().strip().split(' = ')[1].strip("\'"), 16))
    b = literal_eval(f.readline().strip().split(' = ')[1])
    answer = literal_eval(f.readline().strip().split(' = ')[1])

n = 197
m = 19700
R_A = random
R_A.seed(seed)
A = np.array([uniform_sample(n, q, R_A) for _ in range(m)]).tolist()

variables = [f's{i}' for i in range(197)] + ['e']
MY = PolynomialRing(GF(q), variables)
s = vector(MY.gens()[:-1:])
e = MY.gens()[-1]


L, R = [], []
for i in tqdm(range(19700)):
    tmp = (vector(A[i]) * s  + e_L[0] - b[i]) * (vector(A[i]) * s  + e_L[1] - b[i])
    L.append(tmp.coefficients()[:-1])
    R.append(-tmp.coefficients()[-1])
    

L, R = Matrix(GF(q), L), vector(GF(q), R)
my_s = (L.solve_right(R)).list()[-197:]
s = []

#对得到的s做一下调整
for i in my_s:
    if i > q // 2:
        s.append(ZZ(i) - q)
    else:
        s.append(ZZ(i))

print(s == answer)

end_time = time.time()

total_time = end_time - start_time

print(f"运行总时间: {total_time:.2f} 秒")

这边矩阵L和R赋值的时候使用的是单进程的，如果要求速度更快些（像原先的题意那样，可以使用多进程来进行赋值，这样会快很多，但是多进程我写的好像一直有些问题，有没有大佬教教？(●´ω｀●)ゞ）

并非RC4

加密代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
from Crypto.Util.number import *
from sympy import *
import random
from secret import small_key, flag

#你能找到这个实现错在哪吗
def faulty_rc4_encrypt(text):
    data_xor_iv = []
    sbox = []
    j = 0
    x = y = k = 0
    key = small_key
    
    for i in range(256):
        sbox.append(i)
    else:
        for i in range(256):
            j = j + sbox[i] + ord(key[i % len(key)]) & 255
            sbox[i] = sbox[j]  
            sbox[j] = sbox[i]
        else:
            for idx in text:
                x = x + 1 & 255
                y = y + sbox[x] & 255
                sbox[x] = sbox[y] 
                sbox[y] = sbox[x]
                k = sbox[sbox[x] + sbox[y] & 255]
                data_xor_iv.append(idx^k^17)
    return data_xor_iv



def main():
    mt_string = bytes([random.getrandbits(8) for _ in range(40000)])
    encrypted_data = faulty_rc4_encrypt(mt_string)
    
    p = nextprime(random.getrandbits(512))
    q = nextprime(random.getrandbits(512))
    n = p * q
    e = 65537
    
    flag_number = bytes_to_long(flag.encode())
    encrypted_flag = pow(flag_number, e, n)
    
    with open("data_RC4.txt", "w") as f:
        f.write(str(encrypted_data))
    
    print("n =", n)
    print("e =", e)
    print("encrypted_flag =", encrypted_flag)
    
if __name__ == "__main__":
    main()


'''
n = 26980604887403283496573518645101009757918606698853458260144784342978772393393467159696674710328131884261355662514745622491261092465745269577290758714239679409012557118030398147480332081042210408218887341210447413254761345186067802391751122935097887010056608819272453816990951833451399957608884115252497940851
e = 65537
encrypted_flag = 22847144372366781807296364754215583869872051137564987029409815879189317730469949628642001732153066224531749269434313483657465708558426141747771243442436639562785183869683190497179323158809757566582076031163900773712582568942616829434508926165117919744857175079480357695183964845638413639130567108300906156467

'''

这题确实和对称加密没什么关系，首先我们很容易得到思路，应该是要拿到getrandbits生成的这些8位随机数，然后进行MT19937状态的重构，难点就在于如何得到这些随机数

这边我们对sbox进行测试，测试代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from Crypto.Util.number import *
from sympy import *
import random

with open('output1.txt', 'w') as f:
    #你能找到这个实现错在哪吗
    def faulty_rc4_encrypt(text):
        my_test = []
        data_xor_iv = []
        sbox = []
        j = 0
        x = y = k = 0
        key = 'small_key'
        
        for i in range(256):
            sbox.append(i)
        else:
            for i in range(256):
                j = j + sbox[i] + ord(key[i % len(key)]) & 255
                sbox[i] = sbox[j]  
                sbox[j] = sbox[i]
            else:
                for idx in text:
                    x = x + 1 & 255
                    y = y + sbox[x] & 255
                    sbox[x] = sbox[y] 
                    sbox[y] = sbox[x]
                    k = sbox[sbox[x] + sbox[y] & 255]
                    my_test.append(k)
                    data_xor_iv.append(idx^k^17)
        f.write(str(my_test))
        
        
        for i in my_test[::-1]:
            if i != 216:
                print(my_test[::-1].index(i))
                break
        return data_xor_iv



    mt_string = bytes([random.getrandbits(8) for _ in range(40000)])
    encrypted_data = faulty_rc4_encrypt(mt_string)
    encrypted_data

查看一下my_test，我们会发现，他在迭代到两万多次的时候，会趋近于同一个字符，至于是什么，我们可以在0-256进行爆破，因为MT19937是需要32 * 624，也就是19968比特才能还原出状态，对应9比特的话也就是需要2496组，我们取后面的一万组，这完全足够了

然后就是预测的问题，这边我使用的这个板子

1
https://github.com/JuliaPoo/MT19937-Symbolic-Execution-and-Solver

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from Crypto.Util.number import long_to_bytes, inverse
from sympy import nextprime
from ast import literal_eval
from tqdm import trange
import sys



sys.path.append('MT19937-Symbolic-Execution-and-Solver-master/source')
from MT19937 import MT19937

with open('data_RC4.txt', 'r') as f:
    tmp = literal_eval(f.readline())

n = 26980604887403283496573518645101009757918606698853458260144784342978772393393467159696674710328131884261355662514745622491261092465745269577290758714239679409012557118030398147480332081042210408218887341210447413254761345186067802391751122935097887010056608819272453816990951833451399957608884115252497940851
e = 65537
encrypted_flag = 22847144372366781807296364754215583869872051137564987029409815879189317730469949628642001732153066224531749269434313483657465708558426141747771243442436639562785183869683190497179323158809757566582076031163900773712582568942616829434508926165117919744857175079480357695183964845638413639130567108300906156467

for k in trange(256):
    flag = ''
    data = []
    for i in tmp[30000:]:
        data.append(i ^ 17 ^ k)
    try:
        rng = MT19937(state_from_data = (data, 8)) #指定数据是8比特，然后给定数据
        for _ in range(10000):
            rng()
        p, q = '', ''
        for _ in range(512 // 32):
            p = bin(rng())[2::].zfill(32) + p
        for _ in range(512 // 32):
            q = bin(rng())[2::].zfill(32) + q
        p, q = nextprime(int(p, 2)), nextprime(int(q, 2))
        if (p * q == n):
            d = inverse(e, (p - 1) * (q - 1))
            flag = long_to_bytes(pow(encrypted_flag, d, n))
            if flag:
                print(flag)
                break
    except:
        pass

'''
b'VNCTF{FL4w3d_RC4_C0nv3rg3s_2_123_4nd_M1nd_Sm4ller_MT_Brut3}'
'''

更新于：2025年2月14日

评论

评论区